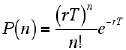
2005年に「計数法における数え落としの補正」として紹介しているように,便利な「数え落としの補正法」を開発しました。しかし,別のページ(最尤推定法, PDF 486kB)に記載したように,数え落としの影響を受けた強度データに対して最尤推定法を適用するためには,統計分布がどのようになるかが明らかになっている必要があります。ここでは,数え落としがある場合に強度データの統計誤差をどのように扱えば良いかについて計算機実験で調べた結果を公開します。
この結果を short communication [Ida, T. (2007). J. Appl. Cryst. 40, 964-965] として発表したものを, ここからダウンロードできます。
物質・材料研究機構の泉富士夫先生(Web Page of Fujio Izumi)によれば, RIETAN-FP では GSAS-ESD 形式の強度データ (int ファイル) を読み込むことができるので, ユーザが強度データ毎に統計誤差を直接指定できるようになっているとのことです。 この機能を使えば,数え落とし補正が施されたデータの統計誤差を正しく考慮したリートベルト解析を行うことができるはずです。
計数法では一定時間にカウントされるパルス数を数えることにより強度を評価します。 個々のパルス発生イベントが独立に生じる場合に, パルス数の統計的な分布はポアソン Poisson 分布にしたがうと考えられます。 平均パルス発生率 r, 計数時間 T の場合に, n パルスが発生する確率は,
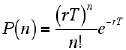 |
(1) |
で与えられます。 ポアソン分布では平均値と分散が厳密に等しいという関係があるので, 観測されるパルス数がポアソン分布に従うとすれば, 観測強度の誤差はカウント数(の平均)の平方根に等しいとみなすことができます。
しかし,現実の検出システムの反応時間は有限なので, 一定の確率で必ず数え落としが生じます。 パルスが発生するイベントが独立に生じるとしても, パルスをカウントするイベントは互いに独立でないということは, 「火を見るより明らか」であり, 実測のカウント数が厳密にはポアソン分布に従うはずがない ということもすぐに想像がつきます。
実測の強度データは,ふつう重みつきの最小二乗法によって解析されます。 この方法では重みつきの残差二乗和
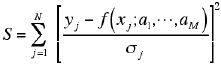 |
(2) |
を最小化する解としてパラメータ (a1, ... , aM) が最適化されます。 ここで yj が実測の強度であり, σj が統計的な誤差です。
統計的な誤差の分布が正規分布あるいはポアソン分布に従うとみなせる場合に, 重み付きの最小二乗法は,「実測データの出現確率が最大となる」という意味で 最尤(いちばんもっともらしい)推定解を与えます。 重みつき最小二乗法を使えば, 誤差の小さい正確なデータを重視して, 誤差の大きい不正確なデータの重みを減らすことができるので, 直観的にも具合が良さそうだと思われます。
計数法により実際に測定された強度データに最尤推定法の考え方を適用するためには, 数え落としの影響を受けた強度データの統計分布について知る必要があります。
伝統的な数え落としモデルである 「非拡張死時間モデル non-extended dead-time model」と「拡張死時間モデル extended dead-time model」 (Quintana, 1991) の考え方については,既に「計数法における数え落としの補正」として別のページに示しました。
死時間を τ とすると,非拡張死時間モデルにより数え落とされた強度データの平均値は
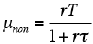 |
(3) |
分散は
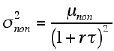 |
(4) |
となることが予想されます。
一方,拡張死時間モデルにより数え落とされた強度データの平均値は
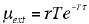 |
(5) |
分散は
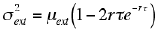 |
(6) |
と近似されることが予想できます。
ただし, これらの式はいずれも計数時間が死時間に比べて無限に長い(T >> τ)極限でのみ成立する式なので, 計数時間が有限な場合に,どのていど適用しうるものなのかが明らかではありませんでした。 そこで,モンテカルロシミュレーションによる計算機実験を行ってみることにしました。
まず,コンピュータを使って,擬似的にポアソン過程に従うパルス列を発生させる方法について考えます。 式 (1) から,パルスの発生がポアソン過程に従う場合に, 一定時間 T の間に1発もパルスが発生しない確率は
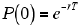 |
(7) |
で与えられます。
つまり,ポアソン過程に従うパルス列とは, パルスの間隔 T の統計的な分布が e-rT の指数分布に従うようなパルス列のことであるとみなすこともできます。
Igor マクロ言語では,"0.5+enoise(0.5)" により 0 から 1 の値をとる一様乱数を発生できるので, "-ln(0.5+enoise(0.5))/r" とすれば e-rT の指数分布に従うような ランダムな時間間隔を発生できます。
この考え方は領域をランダムに分割する場合に一般的に適用できます。 たとえば,結晶中に不整面がランダムに存在する場合に,可干渉性の領域の寸法の統計的な分布は指数分布に従います。 回折ピーク形状は可干渉性領域の自己相関関数のフーリエ変換に対応するので,積層不整によるブロードニングが結果としてローレンツ型関数に近い形になることは容易に推定できます。
Igor マクロ言語を使い,以下のようなコードで非拡張死時間モデルと拡張死時間モデルによる数え落としをシミュレーションしました。
function pnoise()
return -ln(0.5+enoise(0.5))
end;
function count_nonextended(r,T,tau)
variable r,T,tau;
variable t0; // last pulse arrival time
variable tv; // last valid pulse arrival time
variable tc; // current time
variable count=0;
t0=0;
tv=0;
do
tc=t0+pnoise()/r;
if (tc<T)
if (tc>tv+tau)
count+=1;
tv=tc;
endif;
t0=tc;
endif;
while (tc<T);
return count;
end;
function count_extended(r,T,tau)
variable r,T,tau;
variable t0; // last pulse arrival time
variable tc; // current time
variable count=0;
t0=0;
do
tc=t0+pnoise()/r;
if (tc<T)
if (tc>t0+tau)
count+=1;
endif;
t0=tc;
endif;
while (tc<T);
return count;
end;
計数時間 T = 1,死時間 τ = 0.001 としてシミュレーションを行いました。 平均計数率 r を変化させ,各平均計数率の値ごとに 1000 回のシミュレーションを繰り返し,1000個のカウント数データについて平均と分散を求めます。また,各カウント数に対して数え落とし補正をほどこしたデータの分散も計算しました。
非拡張死時間モデルについて,式 (3), (4) から計算された曲線と,シミュレーションの結果得られた結果を図1に示します。図1には誤差伝播則から見積られる「数え落とし補正をほどこした強度の分散」も示しています。
誤差伝播則によれば,実測の強度 y と数え落とし補正を施した強度 z の間に
 |
(8) |
という関係がある場合に,実測の強度の統計誤差 Δy と 数え落とし補正を施した強度が伴う誤差 Δz との間には
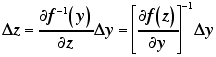 |
(9) |
という関係が成立すると考えられます。
簡便には
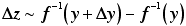 |
(10) |
という式で数え落とし補正後の誤差を見積ることもできます。
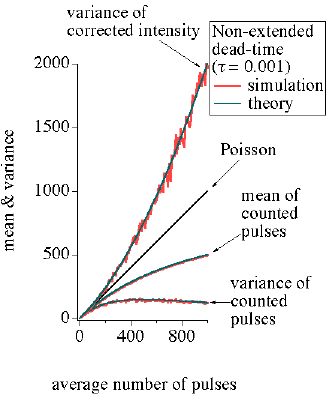
図1:非拡張死時間モデルに関するシミュレーション結果
確かに,式 (3), (4) から計算される曲線は,シミュレーションの結果を良く再現しています。
同じように,拡張死時間モデルについて,式 (5), (6) から計算された曲線と,シミュレーションの結果得られた結果を図2に示します。図2にも誤差伝播則から見積られる「数え落とし補正をほどこした強度の分散」を示しています。
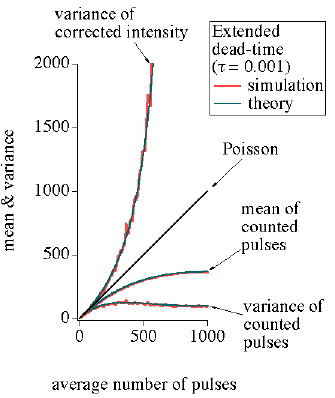
図2:拡張死時間モデルに関するシミュレーション結果
やはり,式 (5), (6) から計算される曲線は,シミュレーションの結果を良く再現しています。
数え落としの影響を受けた実測のカウント数の分散は平均値よりも小さい値になっており,もしこれがポアソン分布に従うと仮定すると統計誤差を過大評価することになりますが,逆に,数え落とし補正をした強度データがポアソン分布に従うと仮定すると統計誤差を過小評価することになることがわかります。
Ida, T. & Iwata Y. (2005). J. Appl. Cryst. 38, 426-432.
Press, W. H., Flannery, B. P., Teukolsky, S. A. and Vetterling, W. T. (1986). Numerical Recipes. Cambridge Univ. Press.
Quintana, J. P. (1991). J. Appl. Cryst., 24, 261-262.
2007年9月21日公開