便利で高精度な「数え落としの補正法」を開発しました。
原著論文 [Ida, T. & Iwata, Y. (2005). J. Appl. Cryst. 38, 426-432] は ここからダウンロードできます。
ところで,皆さんが使っているリートベルト解析や構造精密化の方法は本当にそれで大丈夫でしょうか?
ふつうにX線回折を測定するときに,回折X線の強度は計数法 counting method によって評価します。 X線の光子が検出器(センサ)に当たったときに信号線には電気パルスが発生し, 一定の時間の間に検出される電気パルスを数えれば高感度に回折X線の強度を見積もることができます。
「計数法による強度測定」は高感度なのが良いところですが, もし回折X線が強くてあまり頻繁にパルスが発生するような場合には, 「数え落とし」という現象が現れて実際に検出できるパルスが減ってしまい, 強度が少なめに見積もられてしまうことがあります。
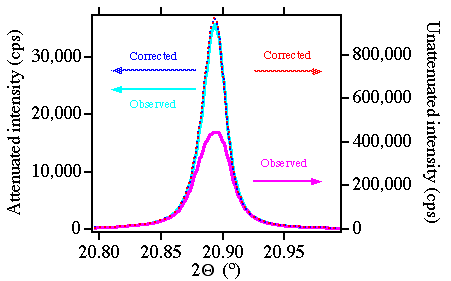
下図に数え落としの例を示します。同じ回折ピークを2回測定し, 「アルミ箔を減衰器 attenuator として光路に挿入して測定した結果」を空色の実線で, 「アルミ箔を挿入しないで測定した結果」をマジェンタの実線で示しています。 アルミ箔を挿入した場合には本来の回折ピーク形状に近い値 (それでも少し数え落とされています)が測定されていると考えられるのですが, アルミ箔を挿入していないと強度が高すぎるので「数え落とし」のせいでピークの頂上付近がつぶれてしまい, 正しいピーク形状からかけ離れたものになっていることがわかります。 ピーク形状が変形してしまっているので,回折ピークの積分強度がずれてしまうだけではなく, ピーク位置も,線幅も数え落としの影響を受けることになります。
ところが,本稿で紹介する方法を使って数え落としの影響を補正すれば, アルミ箔を挿入した場合としていない場合とでそれぞれ青色と赤色の破線で示したように 良く一致したピーク形状が得られます。
ただし,ここで注意しておきたいことは,もし完全に「数え落とし」が補正できたとしても, 補正後の強度が「計数統計誤差」に従うとは考えられないということです。 さらに,実際には完全に「数え落とし」を補正することはできないでしょうから, 「数え落とし補正の誤差」も残るはずです。 リートベルト解析では誤差の要因として「計数統計誤差」を仮定することが多いのですが, 「数え落とし」を補正した場合に残る誤差は「計数統計誤差」とはかなり違ったものになるということを 注意するべきだと思います。 現実の測定装置に数え落としがある以上,それを無視して良いはずはありません。
本稿で紹介する方法を使うことで,はじめて数え落としの影響を正しく評価して, 正しく補正をし,さらに補正後の誤差を正しく評価することが現実に可能になったのではないかと思います。 少し大げさな言い方かもしれませんが, 数え落としの効果を正しく考慮することはX線を使った精密な構造解析のために必須のことですから, この研究の結果, やっとX線回折を使った正しい構造評価をするための第一歩を踏み出すことができるようになったと私自身は思っています。
 |
| 図1.数え落としによる粉末回折ピーク形状の変形。 空色とマジェンタの実線は減衰器を入れた場合と入れない場合の回折ピーク強度の実測値を示す。 破線は数え落とし補正により得られる曲線。 |
数え落としを正しく補正するためには,何が原因で数え落としが生じるのかについて検討する必要があるでしょう。 教科書を見ると数え落としはセンサの「不感時間」で説明されることが多いようですが, 実際にはパルス計数回路の時定数の影響の方が強い場合が多いかもしれません。 X線源としてシンクロトロン軌道放射を使う場合には入射X線そのものがパルス性を持っているので, そのことを考慮に入れる必要もでてくるかもしれません。 また,X線回折ではノイズや高次光の影響を除去するために後述する「パルス高分析 pulse-hight analysis」 という方法を使うことが多いのですが,その場合には数え落としの挙動はさらに複雑なものになります。
「理論的なモデル」に基づいて数え落としを補正するためには沢山のパラメータを決めなければならないので, むしろ「経験的な方法」で装置の数え落とし特性を評価して, それを補正に用いる方が現実的な解決策であるように思います。
数え落としは「非拡張死時間モデル non-extended dead-time model」または「拡張死時間モデル extended dead-time model」 (Quintana, 1991) によってモデル化されることが多いようです。 非拡張死時間モデルでは,イベントが発生すると死時間τを引き起こしますが, その死時間の間に発生した次のイベントは死時間を延長しません。 非拡張死時間モデルを「非麻痺型モデル non-paralyzed model」とか「飽和型モデル saturation model」と呼ぶこともあるようです。 拡張死時間モデルでは,同じイベントがそのイベントの発生した時点からさらにτの分だけ死時間を延長します。 拡張死時間モデルを 「麻痺型モデル paralyzed model」とか「窒息型モデル supporation model」と呼ぶこともあるようです。
非拡張死時間モデルのスループット関数は
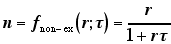 |
(1) |
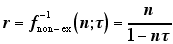 |
(2) |
現実的な検出システムの特性はどちらかというと「拡張死時間モデル」でモデル化した方が良い場合が多いようです
(Omote, 1990; Reed, 1972)。拡張死時間モデルのスループット関数は
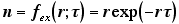 |
(3) |
なお,Cousins (1994) はシンクロトロン軌道放射によるX線を用いた場合について,
以下のスループット関数を提案しました。
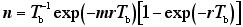 |
(4) |
Cousins (1994) も言及しているのですが,パルス高分析 (PHA) を行う場合には 「許容されるパイルアップ(積み重なり)高さ」によって数え落としの特性が変化します。 パイルアップとは, 近い時間に発生したパルスが重なって見かけ上パルス高が高くなってしまう現象のことを言います。
ここでは単純化したモデルで PHA の影響を議論します
(Cousins は『もう少し現実的かもしれない複雑なモデル』を考えているようなのですが,
そのように複雑なモデルを考える必要はあまりないと思われ,ここで扱うのはもっと単純化したモデルです)。
すべての入力パルスが幅 τw で高さも等しい矩形パルスだとして,
パルスの発生確率は Poisson 過程に従うとします。
すると,PHA の出力は
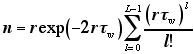 |
(5) |
ところが,式 (5) の形式は以下の式を使えば,
簡単に「整数でない L」にも拡張できることに気がつきました。
|
(6) |
ここで関数 Q(ν,z) は「ルジャンドルの第2種不完全ガンマ関数」とよばれる特殊関数で,
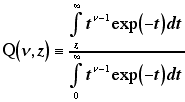 |
(7) |
パイルアップ許容レベル L の値に応じて,式 (6) で表されるスループット関数の形状がどのように変化するかを図2に示します。 お好みならば,この関数を使った最小二乗法で, 実測の数え落とし特性をフィットするように最適化されたパラメータ τw と L の値を求めることができるでしょう。
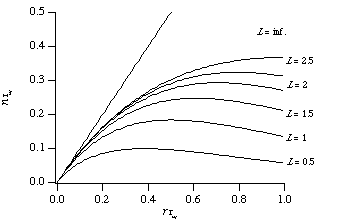 |
| 図2.PHA 窓モデルによる数え落とし曲線。 L が非整数の場合の曲線は L が整数の場合の曲線の中間的な形状になる。 |
さて,許容パイルアップレベルを単パルスの高さに等しくする場合(L = 1),
式 (5) からスループット関数は
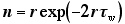 |
(8) |
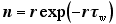 |
(9) |
その一方で,実際の数え落としは PHA だけによるものではなくて, 他のいろいろな要因の影響も受けているはずなので, この関数を用いたフィッティングそのものにはあまり物理的な意味がないかもしれません。 たとえば,もしセンサの不感時間の影響を受けているとすると,PHA に入力されるイベントはもはや Poisson 過程に従っているとみなすことはできないので, このモデル自体の物理的な根拠が薄弱になってしまいます。
Cousins (1994) は,軌道放射光を使って, PHA を使って測定された強度の数え落とし補正の形式を提案しているのですが, 本来 Poisson 過程にしたがっているとみなすことができないイベントについて, Poisson 過程にしたがうものと仮定したモデル化をしてしまっているように思われます。
さて,本当にリアルな意味で正しい数え落としのモデルを理論的に導くのは非常に難しいし,
実際上そんな努力をするのはほとんど無意味だと割り切ってしまうことにします。
さらに,理由は良くわからないのですが,現実の数え落としの挙動が,「非拡張死時間モデル」と
「拡張死時間モデル」との中間的な挙動を示す場合が多いということを前提として,
「中間的な挙動を再現するモデル」をこしらえることにします。
理論的な根拠については深く考えず,単純に「非拡張死時間モデル」と
「拡張死時間モデル」の中間的な挙動を示すモデルの一つの例として,
以下のような形式を思いつきます。
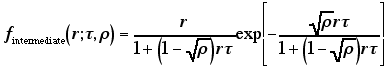 |
(10) |
ただし,この形式は「拡張モデル」と同様に r についての解が得られないので不便です。 次の節では,実際に便利で安心して使えるモデルを提案します。
以下のような便利なモデルを思いつきました。
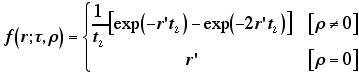 |
(11) |
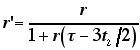 |
(12) |
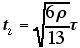 |
(13) |
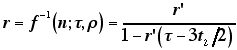 |
(14) |
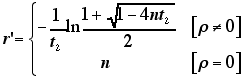 |
(15) |
どうしてこのような近似関数を思いついたか, どうしてこれが極めて良い近似になるのかについても原著論文 (Ida & Iwata, 2005) で説明しています。
減衰器の自動挿入の機構がついていない粉末回折計を使う場合に, 実際にどのような手順で数え落とし特性を評価すれば良いかについても, 論文で記述しています。 手順がわかれば難しくはないのですが, 解析プログラムを完成するにはかなりの時間がかかりました。
ただし,減衰器の挿入を自動制御できれば評価実験も解析ももっと簡単になるはずです。
しかし,新しい装置を作るのはかなり手間がかかるので,製作をする前にコンピュータを使ったシミュレーションをすることにしました。この結果については別の項(計数法における数え落としの補正,その2)で説明します。
実際には減衰器の自動挿入装置を製作するために必要な部品はステッピングモータ/ドライバのセットだけでした。 制御用のパソコンからはパラレルポートからドライバにパルスを送出してモータの回転を制御しました。 この結果として,大量のデータを自動的に収集することが可能になり,数え落としの影響を受けた計数統計誤差に関する実験的な評価が可能になりました。 この結果の説明は準備中です。
Cousins, C. S. G. (1994). J. Appl. Cryst. 27, 159-163.
Ida, T. & Iwata Y. (2005). J. Appl. Cryst. 38, 426-432.
Muller, J. W. (1973). Nucl. Instrum. Methods, 112, 27-57.
Omote, K. (1990). Nucl. Instrum. Methods Phys. Res. Sect. A, 293, 582-588.
Press, W. H., Flannery, B. P., Teukolsky, S. A. and Vetterling, W. T. (1986). Numerical Recipes. Cambridge Univ. Press.
Quintana, J. P. (1991). J. Appl. Cryst., 24, 261-262.
Reed, S. J. B. (1972). J. Phys. E, 5, 994-996.
2010年7月6日修正