数値積分 (numerical integral) を使って「畳み込み」を効率良く計算するための方法を見つけました (Ida, 1998; Ida & Kimura, 1999)。
個々の装置収差を表す装置関数がわかっていれば, 全体の装置関数はそれらを多重に畳み込んだものとして表現されると考えられます。 しかし,実際にそれをどのように計算するかは大問題です。 素朴に考えれば数値積分 (求積法 quadurature) を使って計算できるはずなのですが,
ところが,実際にはなかなかうまくいきません。 どうしてうまくいかないのかというと,
ということが原因です。 数値積分(求積法)は, 積分の中身の関数(被積分関数)を短冊状にスライスして, それを足しあわせて面積を求めるという方法です。 被積分関数に尖ったところがある場合には, 刻みを細かくしていってもなかなか正確な値が求められないのです。
特にピークが鋭い時には特異性 (値や微分が無限大に発散すること) があるのと実際上同じことです。
ところで, 「被積分関数に特異性がある場合には変数変換を使って取り除け」ということは, 数値計算の常識 (伊理・藤野 1985)だと言われています。 何か変数変換を使ったらうまくいかないでしょうか?
また,数値積分では, 被積分関数の形に応じて刻みの幅を変えることによって, 少ない刻みの数でも高精度な結果が得られる場合があります。 このような方法は「ガウス (Gauss) の求積法」と呼ばれ, 例えば, 被積分関数が有限区間で「整級数多項式」近似できる場合に有効な 「ガウス−ルジャンドル (Gauss-Legendre) の求積法」, 無限区間で「整級数多項式とガウス型 (Gaussian) 関数との積」で 近似できる場合に有効な 「ガウス−エルミート (Gauss-Hermite) の求積法」, 半無限区間で「整級数多項式と指数関数との積」で近似できる場合に有効な 「ガウス−ラゲール (Gauss-Laguerre) の求積法」 などがあります (Press et al., 1986)。 畳みこみの計算では2箇所にピークが現れるので, そのままではどれも使えない(使っても意味がない)ことになりますが, この考え方を応用すれば, ピーク付近で刻みの幅を細かくすることができれば, 全体としては少ない刻みの数でも, より正確な値が求められそうです。 これも適切な変数変換を使えば実現できそうに思われます。
効率の良い数値積分を実現するためには, 積分変数を「被積分関数の原始関数に近い値を持つような変数」に変換すれば 良いだろうということは想像がつきます。 もちろん正確な原始関数がわかれば数値積分をするまでもなく, 解けてしまっていることになるわけですが, 正確でなくても原始関数を近似するような関数がわかったら, その値を積分変数にしてやれば計算の効率があがることが期待できます。
ところで,比較的簡単な関数どうしの畳み込みを計算する場合に, 「畳み込まれる2つの関数」のそれぞれについては, 原始関数あるいはその近似形式 が求められることが普通です。 このことを利用できることに気がつきました。
つまり, 以下のような変数変換を使った 置換積分 をしてやれば良いと思われます (Ida, 1998)。
この置換積分の被積分関数の形で, 分母にある関数 G'(...) の中身が, y = 0 のとき 0,y = x のとき x という値を取ることに注目してください。 元の形では鋭いピークになっていた2つの場所で, 変数変換により被積分関数が どちらの場所でも1に近い値になるわけです。 被積分関数が1に近い滑らかな関数になるので, 粗い刻みの数値積分でもそれなりに良い結果が得られることが期待できます。 また,ここでは単に変数変換を使った置換積分をしているだけなので, 刻みを細かくしていけば必ず 厳密解 に近付いていくはずです。
なお,実際の計算は以下の形式で行います。
関数 F(x) と G(x) の 逆関数がわかっていることが必要になります。 ですから,任意の関数を 「原始関数の逆関数がわかっているような関数」あるいはその合成関数によって 近似できるかがポイントになります。
数式だけだとイメージしにくいので, ここでは図を使って説明します。 下の図のようなピーク形状関数:
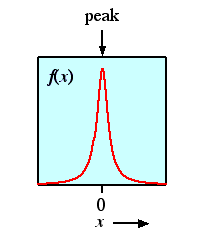
と下の図のような装置関数:
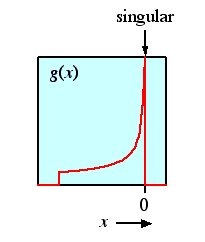
との畳み込みを,数値積分によって計算するためには, 下のような図形の面積を求めなければいけないということになります。
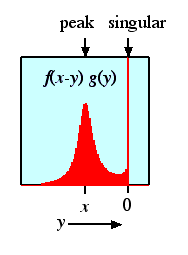
このような変な形になってしまうので, 細かく短冊状にスライスして足し合わせてもなかなか 正解に近付けないということになるわけです。
ところで,先ほどの変数変換を図示すると,下の図のようになります。
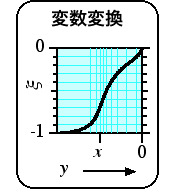
変数 y をξに変換するわけですが, ξについて等間隔な刻みを取ってやれば, 自動的に y についてはピーク位置付近で細かい刻みに なってくれることがわかります。 実際に変数変換をほどこしたあとの置換積分の被積分関数は, 下のような図形になります。
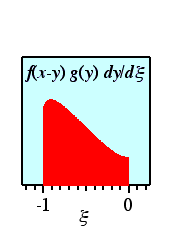
このように,確かに滑らかで, だいたい台形で近似できるような図形になりました。 特異性も取り除かれています。 この場合には台形に近いので,極端な話,中点での値を高さに持つ 長方形の面積を求めてやればほとんど正解に近い値が得られます。 もちろん刻みを細かくしてやれば, どんどん正解に近付いていくはずですし, 有限区間で多項式で近似できるような関数になりましたから, ガウス−ルジャンドル積分を使って効率良く面積を求めることができます。
実際に畳み込みにより表現されるピーク形状を3項の数値積分により 計算した結果を示します。
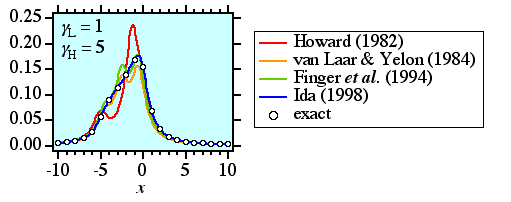
Howard の方法 (1982) は, 装置関数の特異性を変数変換を使って取り除き, あとはシンプソン (Simpson) 積分を使って計算するものです。 厳密解と比べてそれほど見当はずれと言うわけでもないのですが, かなりずれが目立つ結果になっています。
Van Laar & Yelon の方法 (1984) は,変数変換を使わずにそのまま ガウス−ルジャンドル積分を使って計算するものです。 Howard の方法と比べて少しましな結果になっているようにも見えますが, 余計な波打ちが現れていますし, ピーク形状の面積が,正しい値から明らかにずれていることがわかります。 ですから,この関数を使って実測のピーク形状を解析しようとすると, 「必ず積分強度に系統的な誤差が導入される」という致命的な欠点があります。
Finger らの方法 (1994) は, 「変数変換を使わずにそのままガウス−ルジャンドル積分を使って計算した値」 を 「装置関数のみをガウス−ルジャンドル積分を使って積分した値」 で割ってやることにより, ピーク形状の面積については正確な値が得られるように工夫したものです。 ただ,これはいかにも姑息な方法ですね。 得られる形状そのものは van Laar & Yelon の方法と大差なく, やはり余計な波打ちが現れています。 全体として「まあ少しはましかな」という程度で, 「10年も経ってるのにそんなもんかい」というツッコミを入れたくも なってきます。 そもそも,「被積分関数が有限区間で整級数多項式近似できる」という 前提が成り立っていないのですから, ガウス−ルジャンドル積分を使うことは, はっきり言って無意味です (実際,もっと単純な求積法で計算しても結果は大差ありません)。 ガウス−ルジャンドル積分などと言うと, ちょっと高級そうなことをしているらしく見えるところが, 感じが悪いですね。
もちろん以上の方法はいずれも数値積分の項数 (刻みの数)を増やせば正解に近付いていくのですが, 必ず余計な波打ちが残ります。 見た目で目立たない波打ちであっても, ニュートン法を応用した最適化計算の際には微分が効いてくるので, 見た目以上に深刻な問題になりそうです。 実際, Finger らの方法で計算されるモデル関数を使って 実測のピーク形状にあてはめるような計算(カーブフィッティング)をすると, 「なかなか収束しない」とか「発散してしまう」という場合も多いようです。
ところが,図中の青い曲線で示してあるように, 適切な変数変換を使った方法により, ここに示した例の場合には たった3項の数値積分でも見た目で厳密解 と区別できないくらい正確な値が得られます。 計算結果に余計な波打ちが現れないので, カーブフィッティングに応用した場合の収束性も良好です。 何よりも, 「被積分関数の特異性を変数変換を使って取り除く」という 正統な方法に忠実に従っているだけだというところが, 好ましく思われます。
世の中には「畳み込み」を正確に計算したいという場合がかなり多いでしょう。 この計算法は多くの場合に利用できるのではないかと思います。 また,この計算法の考え方自体は, 必ずしも「畳み込み」を計算する場合だけでなく, もっと広く応用の場があるようです。 そのうちの一例を別の項で紹介します。
"A correction for powder diffraction peak asymmetry due to axial divergence", L. W. Finger, D. E. Cox and A. P. Jephcoat, J. Appl. Cryst., 27, 892-900 (1994).
"The approximation of asymmetric neutron powder diffraction peaks by sums of Gaussians", C. J. Howard, J. Appl. Cryst., 15, 615-620 (1982).
"An efficient method for calculating asymmetric diffraction peak profiles", T. Ida, Rev. Sci. Instrum., 69, 3837-3839 (1998).
"Effect of Sample Transparency in Powder Diffractometry with Bragg-Brentano Geometry as a Convolution", T. Ida and K. Kimura, J. Appl. Cryst., 32, 982-991 (1999).
"The peak in neutron powder diffraction", B. van Laar and W. B. Yelon, J. Appl. Cryst., 17, 47-54 (1984).
W. H. Press, B. P. Flannery, S. A. Teukolsky and W. T. Vetterling, Numerical Recipes. Cambridge Univ. Press. (1986).
伊理正夫,藤野和建, 数値計算の常識. 共立出版 (1985).
2007年8月7日修正