粉末回折データから装置収差をデコンボリューションにより除去するための新しい方法を見つけました (Ida & Toraya, 2002)。
効率の良い畳込みの計算法はわかっているのですが, 畳み込みに基づいたピーク形状モデルを, リートベルト法のような全回折パターンのフィッティングなどに用いるには, 計算時間がかかり過ぎるようです。 正統な方法ではないかもしれませんが, フーリエ変換を利用したデコンボリューションの方法を使って, 粉末回折データから装置の影響を除去することができないかを考えてみます。 標準的なデコンボリューションは,「測定データのフーリエ変換」を 「装置関数のフーリエ変換」で割って, さらに逆フーリエ変換するという簡単な手順の計算であり, 高速フーリエ変換 (fast Fourier transform; FFT) アルゴリズム を使える場合には非常に高速に計算できます。
しかし,良く考えてみると,粉末回折計の装置関数は回折角により変化するので, 「個々の回折ピークは装置関数の畳み込みとして表現できる」 けれども 「広い角度範囲にわたる粉末回折データ全体は共通の装置関数との畳み込みとしては表現できない」 ということになります。 つまり畳み込みの関係は局所的には成立しているのですが, 大域的には成立していません。 ですから,標準的なデコンボリューションの方法をそのままでは使えないわけです。
今までは,実測の回折ピーク形状が本質的なピーク形状と装置関数の畳み込みだという関係がかなり厳密に成り立つと思っていたのですが, これはあくまでも近似的な関係にすぎないということがわかります。
ところが,ちょっとした工夫をすれば, 広い回折角にわたる粉末回折データから主要な装置収差のすべてをデコンボリューションにより除去できるということに気がつきました。 この方法自体は非常に一般的に使えるものですが, ここでは Bragg-Brentano 型回折計の装置関数を除去する目的に話を限ることにします。
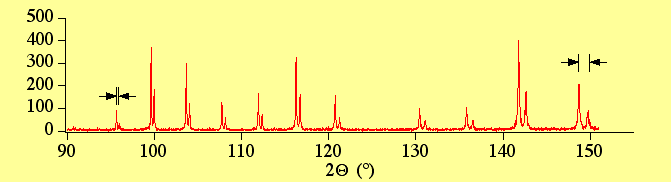
下に典型的な粉末回折データの一部を示します。 六ホウ化ランタン LaB6 の結晶性粉末を, CuKα線源を用いた Bragg-Brentano 回折計で測定したものです。

X線源としてCuKα線を使っているので, 各回折ピークがKα1線とKα2線の2本に分裂しています。 その分裂の幅は低角では狭く, 高角になるほど広がるような変化を示しています。 ですから,X線の分光特性に関して, 全体を共通の装置関数との畳み込みとしては表現できないということがすぐにわかります。
ところが,もし横軸のスケールを変更することが許されるならば, 高角のスケールを縮めてやり,低角のスケールを引き伸ばしてやれば, Kα1線とKα2線の分裂の大きさがどこでも同じになるような絵を描けそうです。 実際,横軸2Θの代わりに ln(sinΘ) というスケールをとって, 上とまったく同じデータを描くと下のような図が得られます。
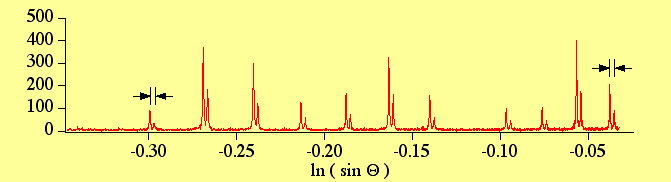
確かに, Kα1線とKα2線の分裂の大きさがどこでも同じになっていることがわかります。 したがって,横軸 ln(sinΘ) というスケールを取れば, X線の分光特性の装置関数に関して大域的な畳込み関係が成立しているということになります。 さらに一般的に,装置関数の回折角による形状変化が, 単純に幅の変化として特徴付けられる場合には, その幅変化に対応したスケール変換を施せば大域的な畳込み関係を成立させることができます。
分光特性の装置関数は幅が tanΘ に比例する形になっています。 そこで「tanΘの逆数の原始関数」である ln(sinΘ) というスケールをとれば, どこをとっても同じ形になるわけです。 同じように,平板試料収差の装置関数は幅が cotΘ に比例しますから, 「cotΘの逆数の原始関数」である -ln(cosΘ) というスケールをとればよいのです。 試料透過性効果の装置関数は,試料が充分に厚い場合に限れば, 幅が sin(2Θ) に比例しますから,その逆数の原始関数 ln(tanΘ) をとればよいはずです。
軸発散収差の装置関数については, 装置関数の回折角による変化は単純に幅の変化のみでは表すことができず, もっと複雑な変化になっています。 ところが幸運なことに,以下のようなことに気がつきました。

つまり,軸発散収差の装置関数を一段階でデコンボリューションにより除去することはできませんが, 二段階にわけてデコンボリューションをほどこせば, やはり同じように除去できるだろうということが予測できます。
以上をまとめると,下の表のようになります。

Bragg-Brentano 回折計の4つの主要な装置収差を, 回折角依存性から3種類に分類することができました。 したがって, 「スケール変換→デコンボリューション→逆スケール変換」 という手続きを3回繰り返せば良いはずです。
なお,元のデータが等間隔だとしても,スケール変換後は等間隔でないので, そのままでは高速フーリエ変換が使えません。 そこで,スケール変換をした後に,補間により等間隔データを作ることにします。 どのように補間するかは悩ましい問題ですが, とりあえず3次スプライン関数 (Press et al. 1986) を使って補間をします。 これで高速フーリエ変換を使えるようになります。
高速フーリエ変換を使えるので, デコンボリューションの計算は非常に高速です。 下に示すのは数千点のデータを同時に処理した例ですが,
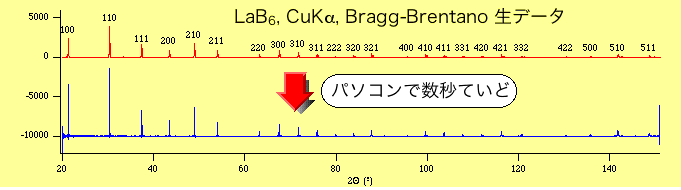
すべての装置収差を除去するために, パソコンを使っても数秒以内ですべての計算が完了します。 このときに,個々の回折ピークの形状が, デコンボリューションによりどのように変化するかを下に示します。
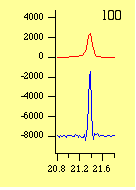
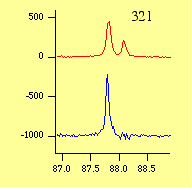
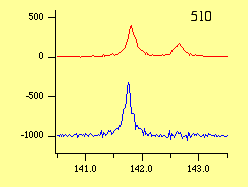
高角でははっきりとKα2ピークが取り除かれていることがわかりますし, 低角では装置の影響で歪んで幅が広いピーク形状だったものが, ほぼ左右対称で鋭いピーク形状に修復できていることがわかります。 デコンボリューション後のデータは全体として, あたかも「現実には存在し得ないような理想的な回折計」で測定されたかのような結果になっています。
デコンボリューション後のデータに対して, さらにカーブフィッティングなどの精密な分析をほどこすためには, そのデータがどのような誤差を伴っているかという情報が重要です。 ところが,私自身は,今までに,「フーリエ法によるデコンボリューションによって 元のデータが含んでいる誤差がどのように伝播するか」 という議論を見たことがありません。 それでも,フーリエ変換はしょせんは線形変換にすぎないのですから, 誤差伝播を評価することもそれほど困難なことではないように思えます。
しかし,ちょっと考えれば, 実験データの含む誤差が相関を持たない場合でも, デコンボリューション後のデータに附属する誤差は相関を持つものになることがわかります。 つまり,誤差が行列の形で表されて,誤差行列の非対角要素がゼロでない値を持つはずです。 原理的には,これをそのままその後のデータ解析に取り入れれば良いのですが, 例えば数千点のデータポイントがあったとして, 行列要素の数は数百万になってしまいますから, かなり厄介な計算になりそうです。
そこで,軽率かもしれませんが, 「非対角要素が値を持つと言ってもやはり対角要素の方が優勢だろうから, 非対角要素を無視してしまって対角要素だけ考えることにしても, 誤差の指標(めやす)くらいにはなるだろう」と考えます。 このように割り切ってしまえば話は簡単で, 誤差行列の対角要素,あるいは誤差行列の逆行列(重み行列)の対角要素だけを 求めればよいことになります。 さらにじっくりと考えると,
になることがわかりました。 悪い冗談のように聞こえるかも知れませんが,高速フーリエ変換を使って 計算することは全然苦になりません。
今のところ,どちらの誤差の指標が良いのか, あるいは中間の値が良いのか, それともどちらもよろしくないのかについてはまだはっきりしていませんが, どちらかというと, 「誤差行列の逆行列の対角要素の逆数の平方根」を取った方が良さそうに見えます (Ida & Toraya, 2002)。 ちなみに,Bragg-Brentano 回折計の装置関数はすべて フーリエ変換が解析的に解ける (Ida & Toraya, 2002) ので, 実際のデコンボリューションの計算には装置関数そのものを使う代わりに, その解析的なフーリエ変換形式を使った方が好都合です。 ということは,……くどいかもしれませんが……, 誤差の指標を求める実際のやり方としては, 「「元のデータが含む誤差の逆数の2乗のフーリエ変換」と 「装置関数のフーリエ変換の逆フーリエ変換の2乗のフーリエ変換の複素共役」の 積の逆フーリエ変換の逆数の平方根」を取れば良かろうということになります。 実は,先程「パソコンで数秒以内で計算が完了する」と書いたのは, この誤差評価の計算まで含めた計算時間です。
この誤差の指標は,絶対値にはやや問題がありそうなのですが, 桁違いというほどではないようですし, どちらかというと誤差を大きく見積もる傾向があるようなので (Ida & Toraya, 2002), とりあえずは無難な誤差評価の方法であると言えます。 また相対的な誤差の挙動を概ね良く表しているようですから, 何か規格化をするような処理をしてやれば, この後の解析で推定されるパラメータの誤差についても, 妥当な値を見積もることができそうです。
粉末回折データについて, フーリエ変換を用いたデコンボリューションの方法を初めて試みたのは, Stokes (1948) によるものだと思われます。 この方法はごく最近でもそのまま使われていて, 「Stokes の方法 (the method of Stokes)」(例えば Langford et al., 2000)とか 「Stokes 補正 (Stokes correction)」(例えば Ungár et al., 2001) として参照されています。 Stokes は,試料を良く焼きなまして結晶性の良い試料を作製して, この「結晶性の良い多結晶体の実測の回折ピーク形状」を, そのまま装置関数の代用として扱っています。 このことで,装置関数の解析的なモデルがわかっていなくても, 形式的にはデコンボリューションによるデータ処理ができるわけです。
このような方法はある意味で無難な面もありますが, 実際には問題がある場合も多そうです。 金属材料ならまだ良いのでしょうが, セラミック材料の場合に焼きなましで結晶性をどこまであげられるかは疑問です。 そしてもちろん, Stokes の方法は全粉末回折データを同時に処理することは不可能で, 1本1本のピークのそれぞれについてデコンボリューションをする必要があるわけです。 このことは,単に面倒臭いというだけでなく, 「ピークの裾の重なりが無視できないような場合には適用できない」 ということになってしまうわけですから, 実際上の応用がかなり限られたものになります。
このようなことを考えれば,我々が提案する 「スケール変換を使った新しい方法」の優位性は明らかであるように思われます。
"Deconvolution of the instrumental functions in powder X-ray diffractometry", T. Ida and H. Toraya, J. Appl. Cryst., 35, 58-68 (2002).
"Effect of a crystallite size distribution on X-ray diffraction line profiles and whole-powder-pattern fitting", J. I. Langford, D. Löuer and P. Scardi, J. Appl. Cryst., 33, 964-974 (2000).
"A numerical Fourier-analysis method for the correction of width and shapes of lines on X-ray powder photographs", A. R. Stokes, Proc. Phys. Soc., 61, 382-391 (1948).
"Crystallite size distribution and dislocation structure determined by diffraction profile analysis: principles and practical application to cubic and hexagonal crystals", T. Ungár, J. Gubicza, G. Ribárik and A. Borbély, J. Appl. Cryst., 34, 298-310 (2001).
2007年8月7日修正