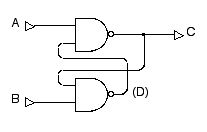
図 2.20 スタティック・メモリ回路
[Next]
[Up]
[Previous]
[Contents]
Next: 2.7.2 ダイナミック・メモリ
Up: 2.7 メモリ
Contents: コンピュータのしくみ
スタティック・メモリは論理ゲートの組み合わせで実現されます。 典型的な例は以下のように2つの NAND ゲートを組み合わせた回路です。

図 2.20 スタティック・メモリ回路
このような回路の出力 C は,2つの入力 A, B によってどのように変化するでしょうか? NAND ゲートのはたらきから,以下の2つの式が成り立ちます。
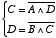 | (2.16) |
この2番目の式を1番目の式に代入すると,
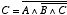 | |
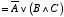 | (2.17) |
という関係が得られます。 2番目の式の変形にはド・モルガンの法則を使いました。 さらに,A と B の値に応じて,C の値がどのような値を取るかを調べると, 以下のようになります。
| A=0, B=0 のとき, | 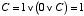 |
| A=1, B=0 のとき, | 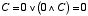 |
| A=0, B=1 のとき, | 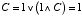 |
| A=1, B=1 のとき, | 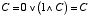 |
つまり,
 | (2.18) |
となります。
この回路の C の値をメモリ(記憶)だとみなすことができます。 A と B はメモリを書き換えるための信号線です。どういうことかということについて,以下に説明します。
通常の状態では A=1, B=1 とします。 はじめは C の値は不定です。 初期化のために「0」というデータを「書き込む」ためには,A=1 に保ったまま B=0 とします。 すると,図 2.21 のように C の値が 0 に変化します。
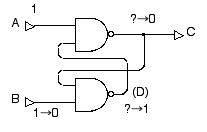
図 2.21 スタティック・メモリ回路に $0$ を書き込む。B を 0 にすれば,必ず C=0 となる。
はじめに,2つある NAND ゲートの下の方を注目してください。 この NAND ゲートの入力の一方が 0 になるので,出力 D は必ず 1 になります。 すると,上の方の NAND ゲートは2つの入力が両方とも 1 になるので,出力 C が 0 になります。
さて,この A=1, B=0 の状態から,はじめと同じ A=1, B=1 の状態に戻したらどうなるでしょうか? 図 2.22 のように,出力は C=0 のままで変化しないことに注目してください。 下の方の NAND ゲートの入力のうちの1つは,今 C=0 になっているので,出力は D=1 のままです。 一方で,上の方の NAND ゲートの2つの入力は両方とも 1 なので, その出力は C=0 でつじつまがあっていることになります。
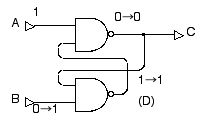
図 2.22 スタティック・メモリ回路に 0 を書き込んだあと, B=0 から B=1 に戻しても,C=0 のままである。
(書き込まれたことを憶えている!)
次に,このメモリに 「1」という値を「書き込む」には,B=1 に保ったまま A=0 とします。 すると,図 2.23 のようになります。上の NAND ゲートの入力の一方が A=0 なので,その出力は C=1 になります。 下の NAND ゲートの入力は B=1, C=1 となるので,その出力は D=0 となります。
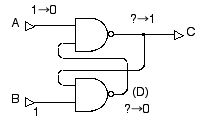
図 2.23 スタティック・メモリ回路に 1 を書き込む。A を 0 にすれば,必ず C が 1 になる。
この後 A=0 から A=1 に戻しても,図 2.24 のように,D=0 なので上の NAND ゲートの出力は C=1 のままです。
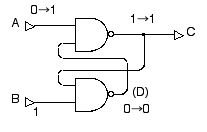
図 2.24 スタティック・メモリ回路に 1 を書き込んだあと,A=0 から A=1 に戻しても C=1 のままになっている。 (書き込まれた値を憶えている!)
このような回路のことをフリップ・フロップ (flip-flop) 回路とかラッチ (ratch) 回路と呼ぶことがあります。 フリップ・フロップとは「ひょいとひっくり返す」といった意味合いの言葉です。 ラッチはラチェット (ratchet) と同じ意味で,逆回りをしないような機構のついた歯車のことです (自転車でペダルを逆に回すと空回りするのはラチェット歯車のはたらきによるものです)。 この電子回路は,確かに機械的なラチェット機構と同じようなはたらきをしていると言えます。
[Next]
[Up]
[Previous]
[Contents]
Next: 2.7.2 ダイナミック・メモリ
Up: 2.7 メモリ
Contents: コンピュータのしくみ