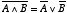
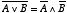
[Next] [Up] [Previous] [Contents]



Contents: コンピュータのしくみ

2.5.2 ド・モルガンの法則 De Morgan's law

法則などというとおおげさな気もするのですが，

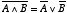	(2.11)
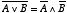	(2.12)

という二つの関係のことをド・モルガンの法則と言います。 前節の「論理演算の規則」を使えば簡単に導くことができますが， 実際に論理演算の中で良く出てくるのでド・モルガンの法則と呼んで使うことにします。 ついでに，次の二つの式もド・モルガンの法則と呼ぶことにしてもよいでしょう。

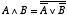	(2.13)
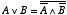	(2.14)

これらの関係も，前節の「論理演算の規則」を使えば簡単に導くことができます。 規則から 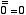, 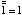だから， 一般的に 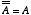と書けることを確認しておいてください。

この法則に何か意味を持たせたければ，たとえば次のような記述を想像してみたらいかがでしょうか？ 「Q君がタワケでもないしアホでもないということはない」 このとき，私がいいたいのは，「Q君はタワケであるかアホであるかのどちらかである」 ということだから，式 (2.14) に対応していますね？

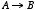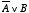余談ですが，「A ならば B である」() ということが， 「AでないかまたはBである」()ということと同じことであるということも， 「Q君はタワケでなければアホである」という言葉が 「Q君はタワケかアホかのどちらかである」ということと同じ意味であると考えれば， 大いに納得できますね。

[Next] [Up] [Previous] [Contents]



Contents: コンピュータのしくみ