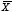 )の規則
)の規則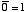
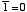
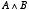 )の規則
)の規則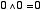
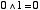
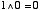
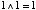
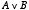 )の規則
)の規則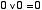
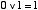
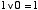
[Next]
[Up]
[Previous]
[Contents]
Next: 2.5.2 ド・モルガンの法則
Up: 2.5 論理回路
Contents: コンピュータのしくみ
後で必要になるので,(あまり厳密ではないのですが)記号論理とか論理代数と呼ばれることがらについての話をします。 現在使われている方法は G. Boole という人が始めたものが元になっており,ブール代数とも良く呼ばれます。
はじめに,形式的な話をします。まず 「0 と 1 の二つの数しかない世界」を考えます。 そして次の3種類の演算(+, −, ×, ÷ のようなもの)の規則をつくります。
(i) NOT 演算(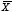 )の規則 )の規則 | |
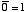 | (2.1) |
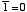 | (2.2) |
(ii) AND 演算(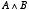 )の規則 )の規則 | |
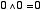 | (2.3) |
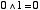 | (2.4) |
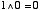 | (2.5) |
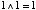 | (2.6) |
(iii) OR 演算(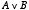 )の規則 )の規則 | |
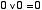 | (2.7) |
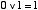 | (2.8) |
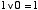 | (2.9) |
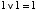 | (2.10) |
この 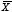 ,
, 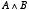 ,
, 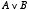 という演算は,
上の規則以外は +, −, ×, ÷ などの計算とまったく同じように扱えるとします。
これを「論理演算」といいます。
どうして論理という名前がついているかというと,
このような一連の規則は,「論理」というものを単純化して扱うことに対応するからでしょう。
という演算は,
上の規則以外は +, −, ×, ÷ などの計算とまったく同じように扱えるとします。
これを「論理演算」といいます。
どうして論理という名前がついているかというと,
このような一連の規則は,「論理」というものを単純化して扱うことに対応するからでしょう。
ところで,「AND 演算」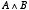 は,0 と 1 の値にしか使わないことを除けば,
「かけ算」
は,0 と 1 の値にしか使わないことを除けば,
「かけ算」 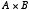 と同じです。
「
と同じです。
「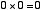 」,「
」,「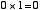 」,「
」,「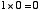 」,「
」,「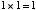 」ですね。
そこで, AND 演算のこと,あるいは AND 演算の結果のことを,論理的なかけ算という意味で「論理積」という言葉で表します。
」ですね。
そこで, AND 演算のこと,あるいは AND 演算の結果のことを,論理的なかけ算という意味で「論理積」という言葉で表します。
「OR 演算」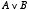 は「たし算」
は「たし算」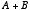 と似ています。
ただし,
と似ています。
ただし,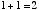 に対して
に対して 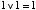 というところが違っています。
それでも,論理的な足し算という意味で「論理和」という言葉が使われます。
というところが違っています。
それでも,論理的な足し算という意味で「論理和」という言葉が使われます。
任意の論理値(つまり 0 か 1 の値)を取る変数を論理変数と呼びます。
たとえば,「今日が休講だということが正しいかどうか」ということを 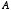 という記号で表して,
「正しい」ということを「
という記号で表して,
「正しい」ということを「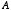 は 1 という値を取る」と言い換えて,
「正しくない」ということを 「
は 1 という値を取る」と言い換えて,
「正しくない」ということを 「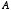 は 0 という値を取る」言い換えることにします。
つまり,今日が休講なら
は 0 という値を取る」言い換えることにします。
つまり,今日が休講なら 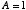 ,休講でなければ
,休講でなければ 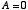 と書くことができます。
と書くことができます。
また,「今日は休講だ」という記述を否定すれば「今日は休講でない」ということになりますから,
「今日は休講でないということが正しいかどうか」ということが 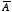 と表されて,
もし今日が休講なら
と表されて,
もし今日が休講なら 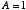 だから
だから 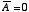 ,
休講でなければ
,
休講でなければ 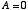 だから
だから 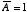 になるということは
1 番目の「 NOT の規則」から確かめることができるでしょう。
になるということは
1 番目の「 NOT の規則」から確かめることができるでしょう。
今度は,「来週は試験だということが正しいかどうか」ということを 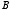 という記号で表せば,
「今日は休講でなおかつ来週は試験だということが正しいかどうか」ということが
という記号で表せば,
「今日は休講でなおかつ来週は試験だということが正しいかどうか」ということが
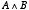 と表されるということになり,
また,「今日が休講であるか来週が試験であるかのどちらかだということが正しいかどうか」ということ
(何が言いたいのかよくわかりませんが)が
と表されるということになり,
また,「今日が休講であるか来週が試験であるかのどちらかだということが正しいかどうか」ということ
(何が言いたいのかよくわかりませんが)が 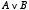 と表されることになります。
と表されることになります。
なんだか,簡単なことをわざと難しくしているように思えなくもないのですが,実際に使う論理演算は, (論理と言う名前はついていますが)必ずしも普通の意味での「論理」と対応づけられなければいけないという必然性はありません。 必要なことは,普通の( +, ー, ×, ÷ などの)計算の規則ではなく,上にあげた「論理演算の規則」に従うということです。 もし頭が混乱してきたら,式 (2.1)〜(2.10) で定義される論理演算の規則に戻って考えるようにしてください。
[Next]
[Up]
[Previous]
[Contents]
Next: 2.5.2 ド・モルガンの法則
Up: 2.5 論理回路
Contents: コンピュータのしくみ