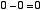
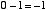
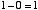
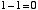
[Up]
[Previous]
[Contents]
Up: 2.8 論理回路による算術演算
Previous: 2.8.1 論理回路による足し算
Contents: コンピュータのしくみ
引き算の結果は負(マイナス)になることもあります。 一般的なディジタルコンピュータでは,負の整数を表現するために「補数表現」という方法を使います。 たとえば 8 ビットの2進数で整数を表現する時に最上位ビットが「0」のときは (00000000)b=0, (00000001)b=1,(00000010)b=2,…, (01111111)b=127 のように普通に値を対応させますが, 最上位ビットが「1」のときは, (10000000)b = -128, (10000001)b=-127,(11111111)b=-1 のように対応させます。 このようにすれば,結果が -128 から 127 の範囲におさまるような足し算は, 前節の足し算回路をそのまま使って計算できます。
補数表現を用いた場合には,有効なビット数によってその意味する値が変わるということに注意する必要があります。 たとえば, (11111111)b は 8 ビットでは -1 という数を表しますが,16 ビットでは 255 という数を表します。
はじめに「2入力1ビット引き算回路」について考えます。つまり,
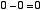 |
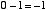 |
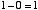 |
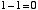 |
という4通りの場合について正しい答えを出力するための回路です。10 進数での 「-1」 という数を,2 ビットの補数表現で 11 と表すことにします。この上位ビットは「繰り下がり」を表すと考えます。この場合,上の例は,
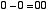 |
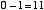 |
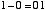 |
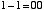 |
と書けます。まとめれば表 2.5 のようになります。
表 2.5 2入力1ビット引き算回路。入力 A,B,
出力 Y0 と繰り下がり Y1
| A | B | Y0 | Y1 |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
また,このような出力を実現する回路を図 2.36 の記号で表すことにします。
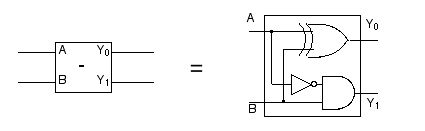
図 2.36「2入力1ビット引き算回路」
さらに,繰り下がりの入力まで考慮して, 3つの1ビット入力 A, B, C から (A - B - C) の結果を出力するような3入力1ビット引き算回路を考えることにします(表 2.6)。 0 - 1 - 1 = -2 ですが,10 進数での「-2」という数は2ビットの補数表現では 「10」と表されます。
表 2.6 3入力1ビット引き算回路。
2j の桁の入力 A,B と 2j-1 の桁の繰り下がり C,
2j の桁の出力 Y0 と繰り下がり Y1
| A | B | C | Y0 | Y1 |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 1 |
| 0 | 1 | 0 | 1 | 1 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 | 1 |
図 2.36 の「2入力1ビット引き算回路」から「3入力1ビット引き算回路」を図 2.37 のように組み立てることができます。
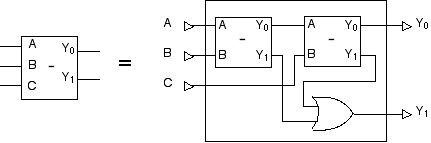
図 2.37「3入力1ビット引き算回路」
さらに,この「3入力1ビット足し算回路を」を必要な数だけ集めれば,任意のビット数の算術的な差を求める回路が作られます(図 2.38)。
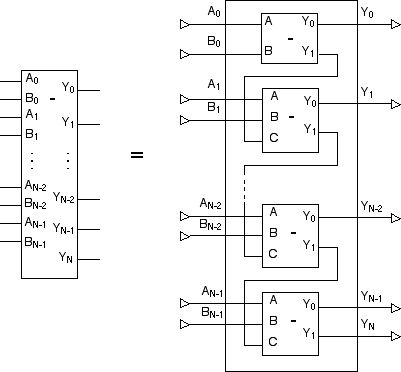
図 2.38「2入力 N ビット引き算回路」
[Up]
[Previous]
[Contents]
Up: 2.8 論理回路による算術演算
Previous: 2.8.1 論理回路による足し算
Contents: コンピュータのしくみ