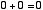
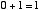
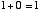
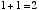
[Next]
[Up]
[Previous]
[Contents]
Next: 2.8.2 論理回路による引き算
Up: 2.8 論理回路による算術演算
Contents: コンピュータのしくみ
2進数の1桁は 0 か 1 の値しかとりません。 この2進数での1桁のことを 「1 ビット bit」といいます。 はじめに,「1 ビットの足し算回路」について考えます。 つまり,
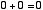 | |
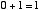 | |
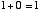 | |
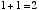 |
という4通りの場合について正しい答えを出力するための回路です。 10 進数での 「2」 という数は2進数だと 「10」 と表されます。 ですから,上の例を2進数で表現すると,
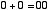 | |
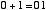 | |
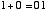 | |
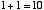 |
と書けます。
このような計算をどのような電子回路で実現できるでしょうか? 中身は後で考えるとして,外から見れば2本の入力信号線と2本の出力信号線を備えた回路になるはずです。 つまり,足し算の2つの入力を A, B という2本の入力信号線に, 出力のうち「20 = 1」の桁の数字を Y0 という出力信号線, 「21 = 2」の桁の数字を Y1 という出力信号線に割り当てます。 全体としては,図 2.32 のような形になるわけです。
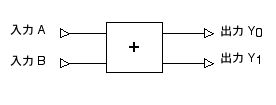
図 2.32 1桁の足し算回路。Y0 は 20 の桁の数,
Y1 は 21 の桁の数を出力する。
つぎに,この回路の中身を考えましょう。出力 Y0 と Y1 とに分けて考えます。 出力 Y0 と入力 A, B の間には表 2.2 のような関係があります。
表 2.2 「1ビット」の足し算回路。入力 A, B と 20 の桁の出力 Y0
| A | B | Y0 |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
この関係を論理式を使って書くために,次のように考えます。 表 2.2 から,「出力が 1 になる」のは,「A=0 かつ B=1」の場合と, 「A=1 かつ B=0」の場合との2通りあります。これを式で表せば,
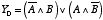 |
となります。 この関係は,図 2.18 の論理ゲートのところに出てきた「排他的論理和 XOR」と同じですね。 つまり,XOR ゲートを使えば「一桁の足し算の 20 = 1 の桁を得る回路」になるわけです。
つぎに,出力 Y1 と入力 A, B の間には表 2.3 のような関係にあります。
表 2.2 「1ビット」の足し算回路。入力 A, B と 21 の桁の出力 Y1
| A | B | Y1 |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
これを式で表せば,
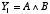 |
となります。
この関係は,「論理積 AND」そのものですね。 つまり,AND ゲートを使えば1桁の足し算の繰り上がりの部分, 21 = 2 の桁を得る回路になるわけです。 これらのことをまとめれば,1ビットの足し算をするための回路としては全体としては,図 2.33 のような構成になります。
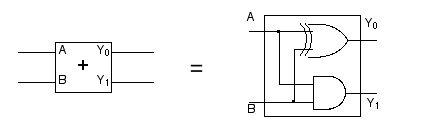
図 2.33 「1ビット」の足し算回路 (2)。XOR ゲートと AND ゲートの組み合わせで実現できる。
次に,任意の桁数の足し算回路について考えましょう。 足し合わせる2つの数が両方とも2進数で N 桁だとします。 つまり,2つの数 A, B がそれぞれ,
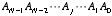 | |
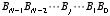 |
のように表されるとします。これらを足し合わせた数 Y は,最大でも N+1 桁にしかなりません。これを
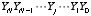 |
と書くことにします。 足し算の結果の 2j の桁の数字 Yj は,Aj と Bj, それと 2j-1 の桁の繰り上がりがあるかどうかによって決まります。 2j の桁の入力を A, B, 2j-1 の桁の繰り上がりを C, 2j の桁の出力を Y0 , 2j の桁の繰り上がりを Y1 と表すことにすれば, 各桁について以下の表で表されるような「3入力1ビット足し算回路」を使えば良いことがわかります。
表 2.4 3入力1ビット足し算回路
| A | B | C | Y0 | Y1 |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
「2入力1ビット足し算回路」を図 2.33 の記号で表すことにすれば, これを使って「3入力1ビット足し算回路」を図 2.34 のように組み立てることができます。
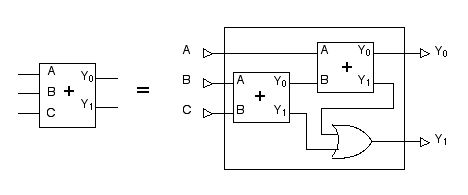
図 2.34「3入力1ビット足し算回路」
さらに,この「3入力1ビット足し算回路を」を必要な数だけ集めれば,
任意のビット数の算術和を求める回路が作られます(図 2.35)。
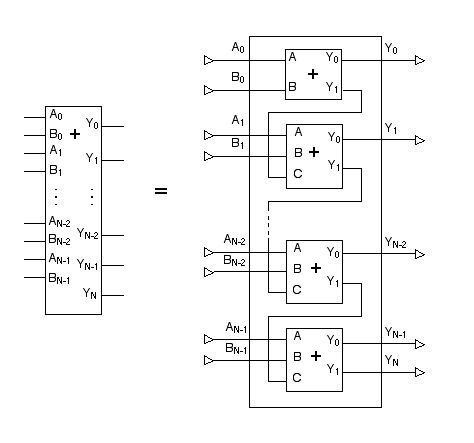
図 2.35「2入力 N ビット足し算回路」
[Next]
[Up]
[Previous]
[Contents]
Next: 2.8.2 論理回路による引き算
Up: 2.8 論理回路による算術演算
Contents: コンピュータのしくみ