）の運動について考えます。
変位（平均位置からのずれ）に対する復元力の強さが変位に比例し
（フックの法則 Hooke's law に従い），
摩擦などの原因により速度に比例する抵抗を受けるような
質点（質量
）の運動について考えます。
変位
が
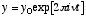
のような式で表されるとします。
記号
は時刻，記号
（ギリシャ文字のニュー）は振動数を表します。
記号
は振幅を表しますが，
複素数でも良いとすれば，位相のずれまで含めることができます。
復元力が
（
は力の定数）と表され，
抵抗は変位
を時刻
で微分したもの（速度）
に比例して
（
はギリシャ文字のガンマ）と表されるとします。
変位
を時刻
で２階微分したもの（加速度）を
と表せば，運動方程式は，
と書けます。このことから，
と書けますが，固有振動数
を定義すれば，
変形して
となります。この式が
以外の解を持つためには，
でなければいけません。このことから，
という２次方程式が導かれ，解の公式から
，
したがって
という式が得られます。
ここで
（
はギリシャ文字のタウ）を定義すれば，
となり，これは振動数
の振動で，
時間
経過するごとに振幅が
倍に，
エネルギーが
倍に減衰するような運動になっていることがわかります。
この
のことを減衰時間とか緩和時間とも言います。
また，このような振動のことを減衰振動 damped oscillation と呼びます。
それでは，外場をかけて強制的に振動させる場合にはどうなるでしょうか？
外場から受ける力は
と表されるとします。運動方程式は
あるいは共鳴振動数
と緩和時間
を使って
と書け，ただちに
と書けます。
さらに，
のときに限定して考えます。
外場の振動数
が共鳴振動数
よりも小さい場合には，
の値は正の実数に近いので，
質点の振動は外場とほぼ同じ位相になります。
低い振動数の交流電場を誘電体に加えた場合の分極はこのような挙動を示します。
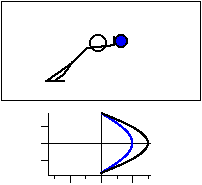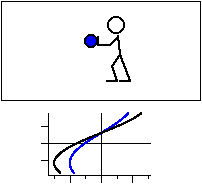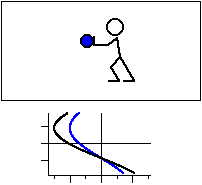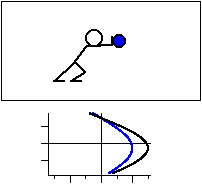
図１ 共鳴振動数よりも低い振動数で振動させる場合。
力の向きを黒線，変位を青線で示す。
加える力の向きと変位の向きは一致する。
ところが，外場の振動数
が共鳴振動数
よりも大きい場合には，
の値が負の実数に近いので，
質点の振動が外場とほぼ逆位相にずれることがわかります。
金属中の自由電子に電磁波をあてた場合には，このような運動をします。
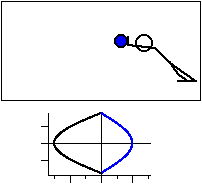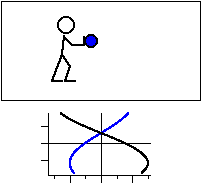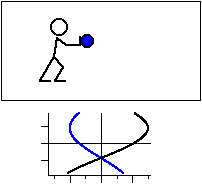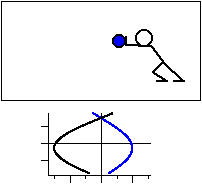
図２ 共鳴振動数よりも高い振動数で振動させる場合。
力の向きを黒線，変位を青線で示す。
加える力の向きと変位の向きは逆になる。
振動数が共鳴振動数と等しい場合（
）には，
となります。
このことは，外場の振動と比べて質点の振動の位相が
ラジアンあるいは
1/4 周期，
遅れることを意味しています。
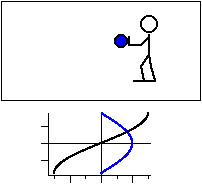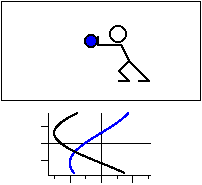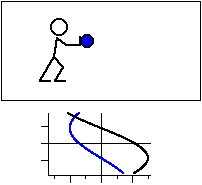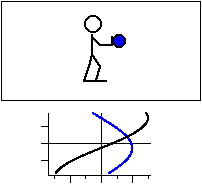
図３ 共鳴振動数と等しい振動数で振動させる場合。
力の向きを黒線，変位を青線で示す。
加える力に対して 1/4 周期遅れた変位が現れる。
2010年7月6日