2つの入力 A, B に対して
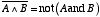 を出力する回路のことを NAND 回路といいます。NAND 回路は図 2.15 のように,2.6.2 節の AND 回路と 2.6.1 節の NOT 回路を
を出力する回路のことを NAND 回路といいます。NAND 回路は図 2.15 のように,2.6.2 節の AND 回路と 2.6.1 節の NOT 回路を組み合わせれば実現できるわけです。
2.6.3 NAND 回路
2つの入力 A, B に対して 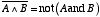 を出力する回路のことを NAND 回路といいます。NAND 回路は図 2.15 のように,2.6.2 節の AND 回路と 2.6.1 節の NOT 回路を
を出力する回路のことを NAND 回路といいます。NAND 回路は図 2.15 のように,2.6.2 節の AND 回路と 2.6.1 節の NOT 回路を
組み合わせれば実現できるわけです。
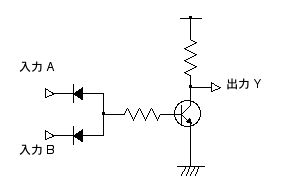
図 2.15 NAND 回路
この回路のはたらきは図 2.16 のように表されます。
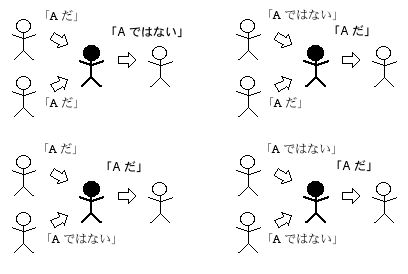
図 2.16 NAND 回路のはたらき
この回路からは 2.6.2 節の AND 回路のようにあいまいな出力ではなく,はっきりした出力を得ることができるので,確かに 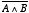 という論理演算に対応したはたらきをします。
という論理演算に対応したはたらきをします。
このようなはたらきをする論理回路のことを論理ゲートといいます。2.6.1 節の NOT 回路は NOT ゲート(インバータ),この節の NAND 回路は NAND ゲートとも呼ばれます。図 2.17 には NAND ゲートの回路記号を示します。
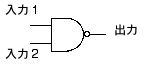
図 2.17 NAND ゲートの回路記号
2.6.4 ゲート素子
論理演算に対応した電子回路をパッケージにしたものをゲート素子と言います。ゲート素子を組み合わせることによって,複雑な論理演算や算術演算も処理することができますし,ある種の記憶素子を実現することができます。代表的な論理ゲートの回路記号を図 2.18 に示します。
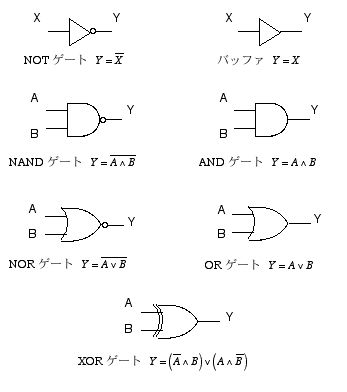
図 2.18 ゲート素子の回路記号
図 2.18 のゲート素子は,いずれも NOT ゲートと NAND ゲートの組み合わせで実現できます。図 2.19 にその例を示します。NAND ゲートは NOT ゲートの代わりに使うことができるので,結局 NAND ゲートの組み合わせだけですべての論理演算を実現できることになります。この意味で,2.6.3 節の NAND ゲートは,他のゲート素子の基本となる重要な素子であると言えます。
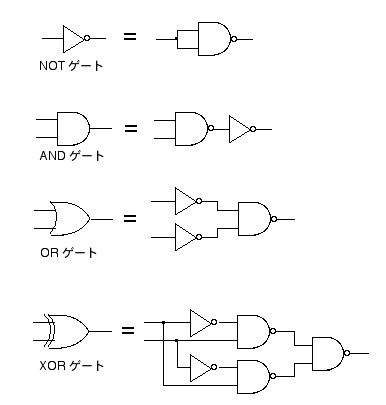
図 2.19 ゲート素子を NAND ゲートと NOT ゲートの組み合わせで作る例
2.7 メモリ
コンピュータはどうやってものを覚えているのでしょうか?電源を入れていない間は磁気ディスクや光ディスクにデータが記録されていることは想像がつくでしょう。これらの装置は「補助記憶装置」と呼ばれます。昔は紙テープやパンチカード,磁気テープなどが補助記憶装置として使われていました。
しかし,データをディスクから読み込んだとしても,主な処理をして次に書き込むまでの間はデータは電子回路に記憶されています。データを記憶しておくための電子回路をメモリと呼びます。原理的には電子回路によるメモリ素子がなくても動作するコンピュータも可能ですが,一般的には補助記憶装置を使ったデータの読み書きよりもメモリ素子を用いたデータの読み書きの方がずっと高速であり,実際上メモリ素子はコンピュータにとって必要不可欠な部品です。
ふつうに使われるメモリ素子には2種類あります。
(1) スタティック・メモリ;S-RAM = Static Random Access Memory
(2) ダイナミック・メモリ;D-RAM = Dynamic Random Acces Memory
これら2種類のメモリ素子は全然違うしくみになっています。詳しいしくみは後述するとして,これらのメモリ素子の特徴を比較すると
表 2.1 のようになります。
表 2.1 スタティック・メモリとダイナミック・メモリの比較
|
素子の |
読み書きの 速さ |
構造の 複雑さ |
高集積 密度化 |
単価 |
| スタティック | 高速 | やや複雑 | やや困難 | やや高価 |
| ダイナミック | やや低速 | 単純 | 容易 | 安価 |
2.7.1 スタティック・メモリ
スタティック・メモリは論理ゲートの組み合わせで実現されます。典型的な例は以下のように2つの NAND ゲートを組み合わせた回路です。
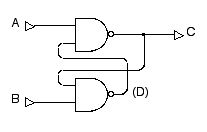
図 2.20 スタティック・メモリ回路
このような回路の出力 C は,2つの入力 A, B によってどのように変化するでしょうか?
NAND ゲートのはたらきから,以下の2つの式が成り立ちます。
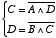
この2番目の式を1番目の式に代入すると,
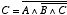
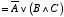
という関係が得られます。2番目の式の変形にはド・モルガンの法則を使いました。さらに,A と B の値に応じて,C の値がどのような値を取るかを調べると,
以下のようになります。
A=0, B=0 のとき,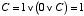
A=1, B=0 のとき,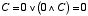
A=0, B=1 のとき,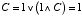
A=1, B=1 のとき,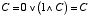
つまり,

となります。
この回路の C の値をメモリ(記憶)だとみなすことができます。A と B はメモリを書き換えるための信号線です。どういうことかということについて,以下に説明します。
通常の状態では A=1, B=1 とします。はじめは C の値は不定です。初期化のために「0」というデータを「書き込む」ためには,A=1 に保ったまま B=0 とします。すると,図 2.21 のように C の値が 0 に変化します。
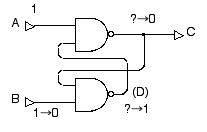
図 2.21 スタティック・メモリ回路に $0$ を書き込む。B を 0 にすれば,必ず C=0 となる。
はじめに,2つある NAND ゲートの下の方を注目してください。この NAND ゲートの入力の一方が 0 になるので,出力 D は必ず 1 になります。すると,上の方の NAND ゲートは2つの入力が両方とも 1 になるので,出力 C が 0 になります。
さて,この A=1, B=0 の状態から,はじめと同じ A=1, B=1 の状態に戻したらどうなるでしょうか?図 2.22 のように,出力は C=0 のままで変化しないことに注目してください。下の方の NAND ゲートの入力のうちの1つは,今 C=0 になっているので,出力は D=1 のままです。一方で,上の方の NAND ゲートの2つの入力は両方とも 1 なので,その出力は C=0 でつじつまがあっていることになります。
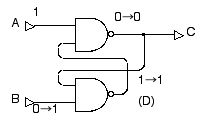
図 2.22 スタティック・メモリ回路に 0 を書き込んだあと, B=0 から B=1 に戻しても,C=0 のままである。 (書き込まれたことを憶えている!)
次に,このメモリに 「1」という値を「書き込む」には,B=1 に保ったまま A=0 とします。すると,図 2.23 のようになります。上の NAND ゲートの入力の一方が A=0 なので,その出力は C=1 になります。下の NAND ゲートの入力は B=1, C=1 となるので,その出力は D=0 となります。
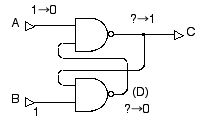
図 2.23 スタティック・メモリ回路に 1 を書き込む。A を 0 にすれば,必ず C が 1 になる。
この後 A=0 から A=1 に戻しても,図 2.24 のように,D=0 なので上の NAND ゲートの出力は C=1 のままです。
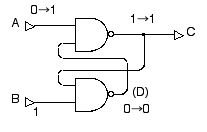
図 2.24 スタティック・メモリ回路に $1$ を書き込んだあと,A=0 から A=1 に戻しても C=1 のままになっている。(書き込まれた値を憶えている!)
このような回路のことをフリップ・フロップ (flip-flop) 回路とかラッチ (ratch) 回路と呼ぶことがあります。フリップ・フロップとは「ひょいとひっくり返す」といった意味合いの言葉です。ラッチはラチェット (ratchet) と同じ意味で,逆回りをしないような機構のついた歯車のことです(自転車でペダルを逆に回すと空回りするのはラチェット歯車のはたらきによるものです)。この電子回路は,確かに機械的なラチェット機構と同じようなはたらきをしていると言えます。
2.7.2 ダイナミック・メモリ
ダイナミック・メモリ素子は,大雑把に言えばキャパシタ(コンデンサ)に
静電気をためることでデータを記憶します。キャパシタの構造は,図 2.25 のように2枚の金属板を向い合せに近づけて配置したものです。
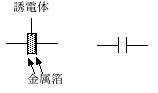
図 2.25 キャパシタ (コンデンサ) の構造 (左) と回路記号 (右)
このキャパシタとダイオード,抵抗を図 2.26 のように組み合わせれば,これがダイナミック・メモリ回路として働きます。キャパシタに電荷がたまっているかどうかで 1 か 0 の値が表されます。
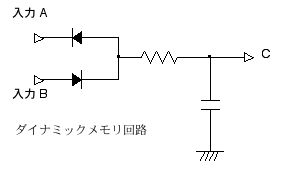
図 2.26 ダイナミック・メモリ回路。通常は A=1 (例えば +5 V), B=0 (0 V) とする。
ダイナミック・メモリ回路の入力信号は,通常は例えば A=+5 V, B=0 V という状態にしておきます。このまま長い間ほうっておけば, C=+2.5 V になるはずです。
ダイナミック・メモリに「0」という値を書き込むには,B=0 を保ちながら A=0 とします。キャパシタから A へ電流が流れることにより放電して,C=0 という状態になります (図 2.27)。
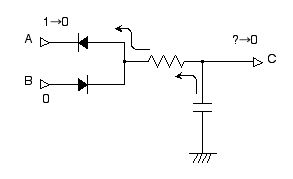
図 2.27 ダイナミック・メモリ回路に $0$ を書き込む。A を 1 から 0 に変化させれば,矢印の向きに電流が流れて $C=0$ となる。
この後に A=1 に戻しても,A から C の方向へは電流が流れにくいので,C=+2.5 V という状態にまで戻るには時間がかかります。つまり,しばらくは「0」という値を憶えていることになります (図 2.28)。
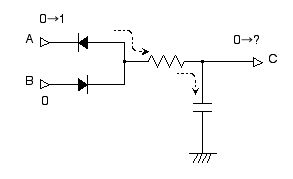
図 2.28 ダイナミック・メモリ回路は 0 という値を憶えている。A を 0 から 1 に戻しても,矢印の向きには電流が流れにくいので,しばらくは C=0 のままである。
ダイナミック・メモリ回路に「1」という値を書き込むには,A=1 を保ちながら B=1 とします。このとき,B から電流が流れ込んでキャパシタに電荷が蓄えられ C=1 という状態になります (図 2.29)。
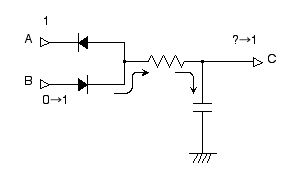
図 2.29 ダイナミック・メモリ回路に 1 を書き込む。B を 0 から 1 に変化させれば,
矢印の向きに電流が流れて C=1 となる。
この後に B=0 という状態に戻しても C から B の方向へは電流が流れにくいので,C=1 という状態がしばらくは保持されます (図 2.30)。
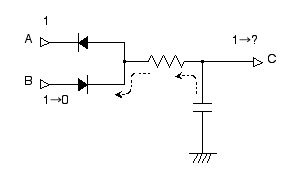
図 2.30 ダイナミック・メモリ回路は 1 という値を憶えている。B を 1 から 0 に戻しても,矢印の向きには電流が流れにくいので,しばらくは C=1 のままである。
ただし,通常の A=1, B=0 の状態でも,キャパシタは少しずつ放電してしまいます。そこで,データを書き込んで一定の時間が経過したら,一度 C の値を読み込んで,もう一度書き込み直すという動作 (リフレッシュ refresh 動作) が必要になります。ふつうのメモリ素子では 1 秒間に数万回くらい (数十 μs に一回) リフレッシュ動作をしているそうです。
2.8 論理回路による算術演算
(ディジタル) コンピュータでは数値を2進数で表しています。ふつうに市販されているコンピュータは,すべてディジタル・コンピュータですが,アナログ・コンピュータというものもあります。
アナログ回路で計算する一つの典型的な方法を紹介します。例えば 「3 で割る」 という計算をしたいときには,図 2.31 のように,抵抗の大きさが 2:1 になるような2つの抵抗を直列につなげば良いだけです。割る数を変えたければ,抵抗の大きさを変えられるような,可変抵抗 (ボリューム) を使えば良いというわけです。
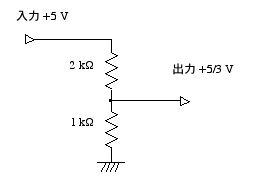
図 2.31 素朴な割り算回路。入力電圧を 3 で割った電圧が出力される。
もっと一般的に,アナログ回路で計算をしやすくするための回路をパッケージにした素子として「演算増幅器」(通称 オペ・アンプ; operational amplifier) というものがあります。精度にもよりますが,普通のものだと1個 100 円くらいで売っています。オペ・アンプを使って加減乗除の計算をするための回路は良く知られています。計測回路などでは「精度は必要ないが,とにかく高速に計算したい」という場合が結構ありますので,知っておいても損はないでしょう。
以下では,ディジタル・コンピュータを使った計算のしかたを紹介します。普通の加減乗除の計算のことを「算術演算 arithmetic operation」と言います。ディジタル・コンピュータでは数値を2進数を使って表します。2進数の算術演算は,前に説明した「論理演算 logical operation」の組み合わせで実現できます。
2.8.1 論理回路による足し算
2進数の1桁は 0 か 1 の値しかとりません。この2進数での1桁のことを 「1 ビット bit」といいます。はじめに,「1 ビットの足し算回路」について考えます。つまり,
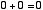
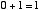
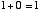
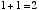
という4通りの場合について正しい答えを出力するための回路です。10 進数での 2 という数は2進数だと 10 と表されます。
ですから,上の例を2進数で表現すると,
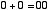
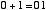
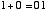
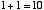
と書けます。
このような計算をどのような電子回路で実現できるでしょうか?おおまかには,2本の入力信号線と2本の出力信号線を備えた回路になるはずです。つまり,足し算の2つの入力を A, B という2本の入力信号線に,出力のうち「20 = 1」の桁の数字を Y0 という出力信号線, 「21 = 2」の桁の数字を Y1 という出力信号線に割り当てます。全体としては,図 2.32 のような形になるわけです。
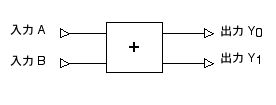
図 2.32 1桁の足し算回路。Y0 は 20 の桁の数,Y1 は 21 の桁の数を出力する。
つぎに,この回路の中身を考えましょう。出力 Y0 と Y1 とに分けて考えます。
出力 Y0 と入力 A, B の間には表 2.2 のような関係があります。
表 2.2 「1ビット」の足し算回路, 20 の桁の出力 Y0
| A | B | Y0 |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
この関係を論理式を使って書くために,次のように考えます。表 2.2 から,「出力が 1 になる」のは,「A=0 かつ B=1」の場合と,「A=1 かつ B=0」の場合との2通りあります。これを式で表せば,
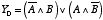
となります。
この関係は,図 2.18 の論理ゲートのところに出てきた「排他的論理和 XOR」と同じですね。つまり,XOR ゲートを使えば一桁の足し算の 20 = 1 の桁を得る回路になるわけです。
つぎに,出力 Y1 と入力 A, B の間には表 2.3 のような関係にあります。
表 2.2 「1ビット」の足し算回路, 21 の桁の出力 Y1
| A | B | Y1 |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
これを式で表せば,
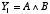
となります。
この関係は,「論理積 AND」そのものですね。つまり,AND ゲートを使えば1桁の足し算の繰り上がりの部分, 21 = 2 の桁を得る回路になるわけです。
これらのことをまとめれば,1ビットの足し算をするための回路としては全体としては,図 2.33 のような構成になるわけです。
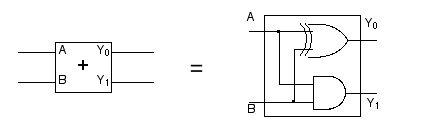
図 2.33 「1ビット」の足し算回路 (2)。XOR ゲートと AND ゲートの組み合わせで実現できる。
次に,任意の桁数の足し算回路について考えましょう。足し合わせる2つの数が両方とも2進数で N 桁だとします。つまり,2つの数 A, B がそれぞれ,
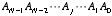
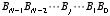
のように表されるとします。これらを足し合わせた数 Y は,最大でも N+1 桁にしかなりません。これを
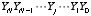
と書くことにします。
足し算の結果の 2j の桁の数字 Yj は,Aj と Bj,
それと 2j-1 の桁の繰り上がりがあるかどうかによって決まります。
2j の桁の入力を A, B, 2j-1 の桁の繰り上がりを C,
2j の桁の出力を Y0 ,
2j の桁の繰り上がりを Y1 と表すことにすれば,
各桁について以下の表で表されるような「3入力1ビット足し算回路」を使えば良いことがわかります。
表 2.4 3入力1ビット足し算回路
| A | B | C | Y0 | Y1 |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
「2入力1ビット足し算回路」を図 2.33 の記号で表すことにすれば,
これを使って「3入力1ビット足し算回路」を図 2.34 のように組み立てることができます。
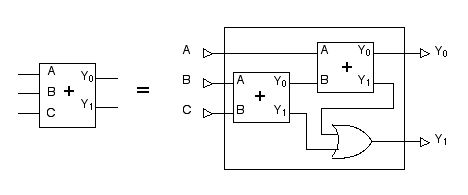
図 2.34「3入力1ビット足し算回路」
さらに,この「3入力1ビット足し算回路を」を必要な数だけ集めれば,
任意のビット数の算術和を求める回路が作られます(図 2.35)。
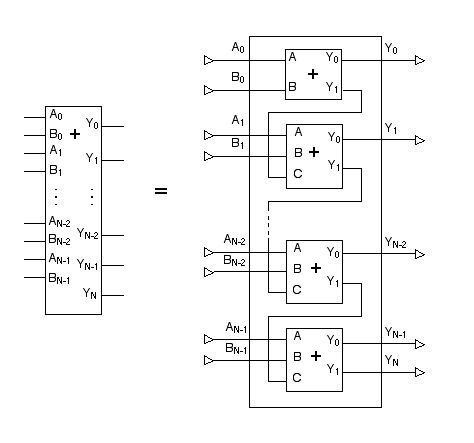
図 2.35「2入力 N ビット足し算回路」
引き算の結果は負(マイナス)になることもあります。 一般的なディジタルコンピュータでは,負の整数を表現するために「補数表現」という方法を使います。 たとえば 8 ビットの2進数で整数を表現する時に最上位ビットが「0」のときは (00000000)b=0, (00000001)b=1,(00000010)b=2,…, (01111111)b=127 のように普通に値を対応させますが, 最上位ビットが「1」のときは, (10000000)b = -128, (10000001)b=-127,(11111111)b=-1 対応させます。 このようにすれば,結果が -128 から 127 の範囲におさまるような足し算は, 前節の足し算回路をそのまま使って計算できます。 補数表現を用いた場合には,有効なビット数によってその意味する値が変わるということに注意する必要があります。 たとえば, (11111111)b は 8 ビットでは -1 という数を表しますが,16 ビットでは 255 という数を表します。
はじめに「2入力1ビット引き算回路」について考えます。つまり,
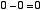 |
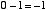 |
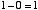 |
align="center"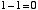 |
という4通りの場合について正しい答えを出力するための回路です。10 進数での 「-1」 という数を,2 ビットの補数表現で 11 と表すことにします。この上位ビットは「繰り下がり」を表すと考えます。この場合,上の例は,
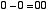 |
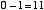 |
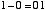 |
align="center"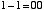 |
と書けます。まとめれば表 2.5 のようになります。
表 2.5 2入力1ビット引き算回路。入力 A,B,
出力 Y0 と繰り下がり Y1
| A | B | Y0 | Y1 |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
また,このような出力を実現する回路を図 2.36 の記号で表すことにします。
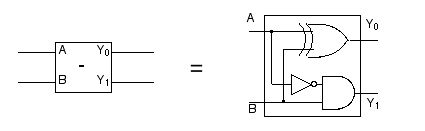
図 2.36「2入力1ビット引き算回路」
さらに,繰り下がりの入力まで考慮して, 3つの1ビット入力 A, B, C から (A - B - C) の結果を出力するような3入力1ビット引き算回路を考えることにします(表 2.6)。 0 - 1 - 1 = -2 ですが,10 進数での「-2」という数は2ビットの補数表現では 「10」と表されます。
表 2.6 3入力1ビット引き算回路。
2j の桁の入力 A,B と 2j-1 の桁の繰り下がり C,
2j の桁の出力 Y0 と繰り下がり Y1
| A | B | C | Y0 | Y1 |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 1 |
| 0 | 1 | 0 | 1 | 1 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 | 1 |
図 2.36 の「2入力1ビット引き算回路」から「3入力1ビット引き算回路」を図 2.37 のように組み立てることができます。
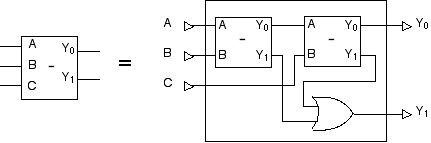
図 2.37「3入力1ビット引き算回路」
さらに,この「3入力1ビット足し算回路を」を必要な数だけ集めれば,任意のビット数の算術的な差を求める回路が作られます(図 2.38)。
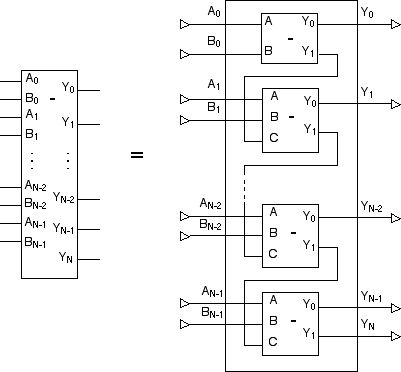
図 2.38「2入力 N ビット引き算回路」
2.8.3 論理回路によるかけ算,割り算
日本の初等教育では,かけ算を九九(くく)を使って計算する方法を学びます。これは十進法で数を表すからで,数を二進法で表すことにすれば 1×1=1 だけ憶えれば良いことになります。後は「桁をずらす」ということと「和をとる」ということができればよいので,電子回路を使って計算することは容易でしょう。
九九を知らなくてもかけ算はできます。別名もあるようですが,「ロシア農民のかけ算」として知られている方法が有名です。
たとえば,19 × 25 という計算をしてみます。はじめに 19 と 25 を横に並べて書いて,次の行には19 を 2 で割った数 9(あまりは無視する;以下同じ)と 25 に 2 をかけた数 (あるいは 25+25)50 を並べて書きます。その次の行には 9 を 2 で割った数 4 と 50 に 2 をかけた数 100 を書きます。どんどん繰り返していって,左側の数が 1 になるまで繰り返します。最後に,左側の数が奇数となっている行の右側の数を足してやればかけ算の答えになる,という方法です。
19 ○ 25
9 ○ 50
4 100
2 200
1 ○ 400
25 + 50 + 400 = 475
ここで,19 を 2 で割っていって奇数かどうかを調べる操作は,二進法表記を下位ビットから順に求めていくことと同じです。ここでは 10011 となります。このことは,
19 = 24 + 21 + 20 と同じ意味です。ロシア農民のかけ算では,下の式で表されるような方法で計算をしていると考えれば良いでしょう。
19 × 25 = (24 + 21 + 20) × 25
= 25×24 + 25×21 + 25×20
= 400 + 50 + 25
実際のコンピュータでどのようにかけ算を実現するかにはいろいろなバリエーションが考えられます。九九と同じように表を使った計算方法が使われる場合もあるようです。いずれにしても電子回路を使ってかけ算をすることができるわけです。